Notes On Collaborative Filtering
-
This is the “Probabilistic Matrix Factorization” method for Recommendation systems.
-
Item and User are the two main inputs required and the learner should be able to recommend Items to Users and vice-versa.
-
Example – Item can be Product and User can be Customer (say Amazon)
-
Another example – Item can be Movie and User can be a Viewer (say Netflix)
-
-
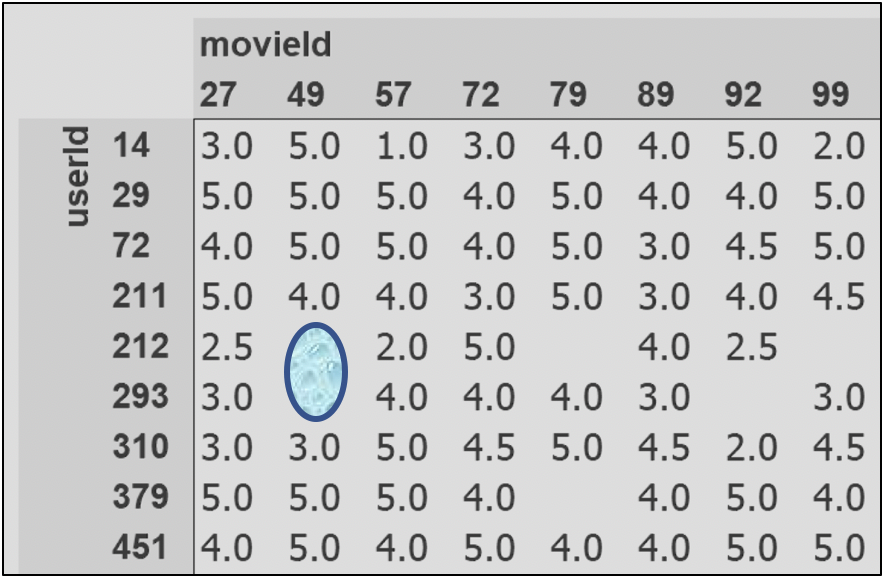
To understand how this works – imagine the data of items and users as a cross-tab report
-
The intersection of each item and user can capture some useful information like product rating/number of times the product was bought or movie ratings/number of times the movie was played.
-
We can predict the gaps in the cross-tab above using collaborative filtering.
-
How much does User 212 going to rate Movie 49 ?
-
Based on this, can we recommend this Movie to him on his home screen ?
-
-
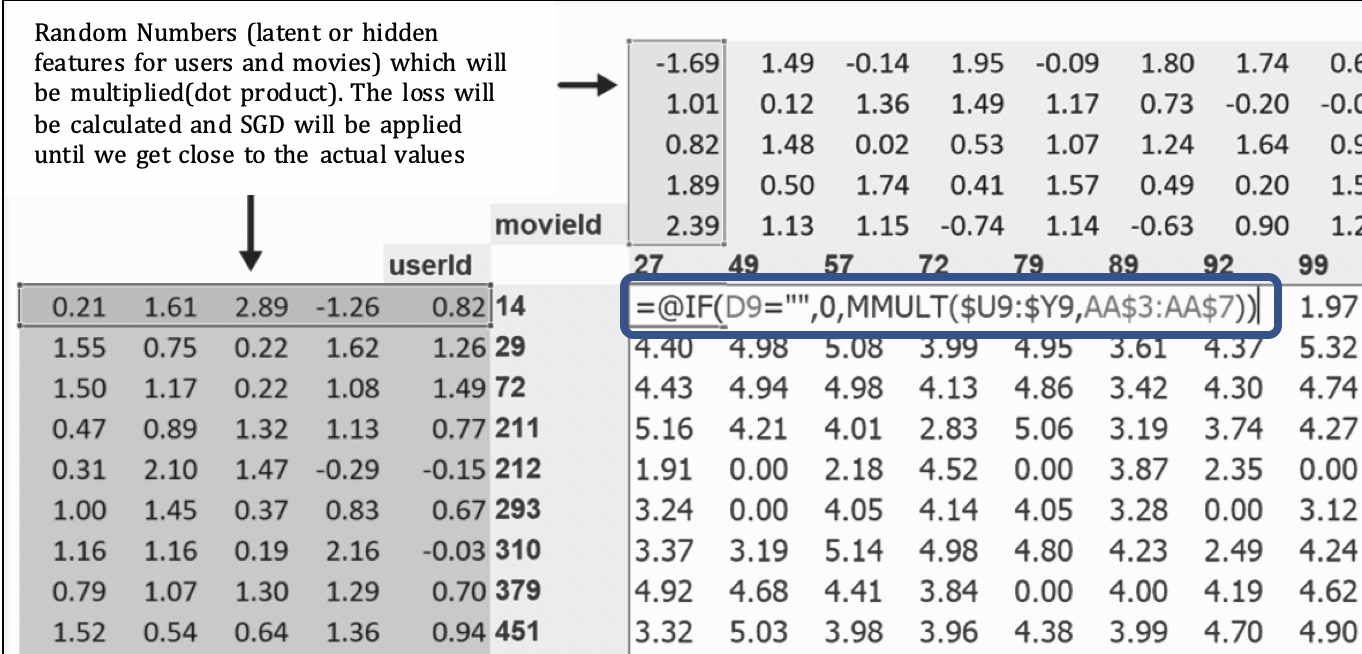
This method works in normal programming but for deep learning this method of doing a dot product of an individual user and a particular movie cannot be done since it required looking up a particular row of data from each latent factor matrix. This would not help with Gradient Descent which is a must for Deep Learning.
-
However, we can implement the same using a one hot encoded matrix. A matrix multiplication of user latent factor matrix and one hot encoded matrix will return only that row where the value is 1. Remember that one hot encoded matrix will have 0s most of the places and 1 in one particular cell. Gradient Descent can happen on this.
-
But, this is computationally a waste since the one hot encoded matrix is mostly 0s and doing this multiplication for large latent features matrices is not practiced. Instead an embedding is used. What is Embedding ?
-
Most deep learning libraries, including PyTorch, include a special layer that does the above step i.e. it indexes into a vector using an integer, but has its derivative calculated in such a way that it is identical to what it would have been if it had done a matrix multiplication with a one-hot-encoded vector. This is called an “Embedding”
-
We also need to add bias for users and a bias for movies since some users are movie aficionados and like most movies or vice-versa and some movies are just something which everyone likes or vice-versa. These biases need to be added to the dot product calculated in above steps.
-
The final layer of the model should also pass through a sigmoid of (a,b) to make sure the values are within the range that we need.
- For example, for a movie rating, if it should be within 1 to 5, we need pass through a sigmoid of (0,5.5). Since sigmoid never reaches 0 or 5.5 we have done this. If we did (1,5) there will not be any ratings with 1 or 5 which we do not want.
-
Weight Decay is a regularization technique to make the loss function less sharp and less narrow. It penalizes by adding sum(square of the weights) to Loss function.